5 Samplers and Solvers
The point of writing a generate model is typically not to simply run
it to generate data, but rather to do inference on it—
A sampler is an object that contains a probabilistic program and produces samples from the posterior distribution of its result expression. Samplers can be either unweighted (where each sample is equally representative of the posterior distribution) or weighted (where each sample comes with a factor that corrects for the ratio of its sampling frequency and its probability in the posterior distribution).
rejection-sampler —
unweighted sampler, does not support observations on continuous random variables importance-sampler —
weighted sampler mh-sampler —
unweighted sampler, uses MCMC to seek high-probability zones
enumerate —
exhaustive enumeration (up to optional threshold), exponential in number of random variables, cannot handle sampling from continuous random variables
The examples in the following sections use the following function definitions:
> (define (count-heads n) (if (zero? n) 0 (+ (if (flip) 1 0) (count-heads (sub1 n)))))
> (define (geom) (if (flip) 0 (add1 (geom))))
5.1 Basic Sampler Functions
A sampler is also an applicable object. That is, if s is a sampler, then evaluating (s) generates a sample.
procedure
(weighted-sampler? v) → boolean?
v : any/c
Every sampler is also a weighted sampler; the samples it produces always have weight 1.
procedure
(generate-samples s n [ f #:burn burn #:thin thin]) → (vectorof any/c) s : weighted-sampler? n : exact-nonnegative-integer? f : (-> any/c any/c) = values burn : exact-nonnegative-integer? = 0 thin : exact-nonnegative-integer? = 0
The sampler is first called burn times and the results are discarded. In addition, the sampler is called thin times before every sample to be retained.
procedure
(generate-weighted-samples s n [ f #:burn burn #:thin thin]) → (vectorof (cons/c any/c (>=/c 0))) s : weighted-sampler? n : exact-nonnegative-integer? f : (-> any/c any/c) = values burn : exact-nonnegative-integer? = 0 thin : exact-nonnegative-integer? = 0
procedure
(sampler->discrete-dist sampler n [ f #:burn burn #:thin thin]) → discrete-dist? sampler : weighted-sampler? n : exact-positive-integer? f : (-> any/c any/c) = (lambda (x) x) burn : exact-nonnegative-integer? = 0 thin : exact-nonnegative-integer? = 0
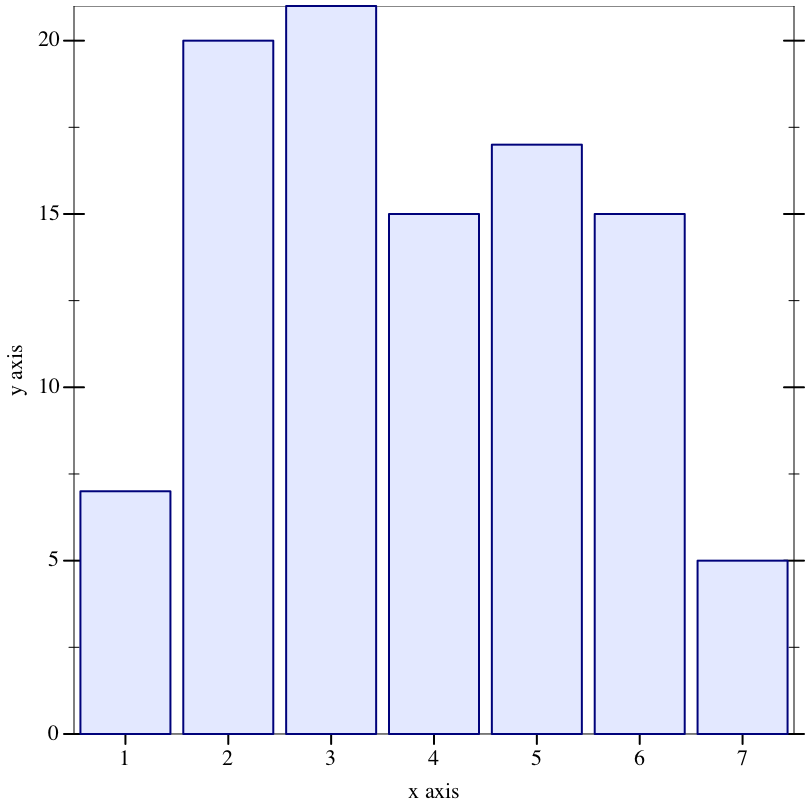
Examples: | ||||||||||||||||||||||
|
5.2 Basic Sampler Forms
The samplers supported by this language consist of simple samplers and a more complicated and flexible Metropolis-Hastings sampler framework.
syntax
(rejection-sampler def/expr ... result-expr)
The sampler is implemented using rejection sampling—
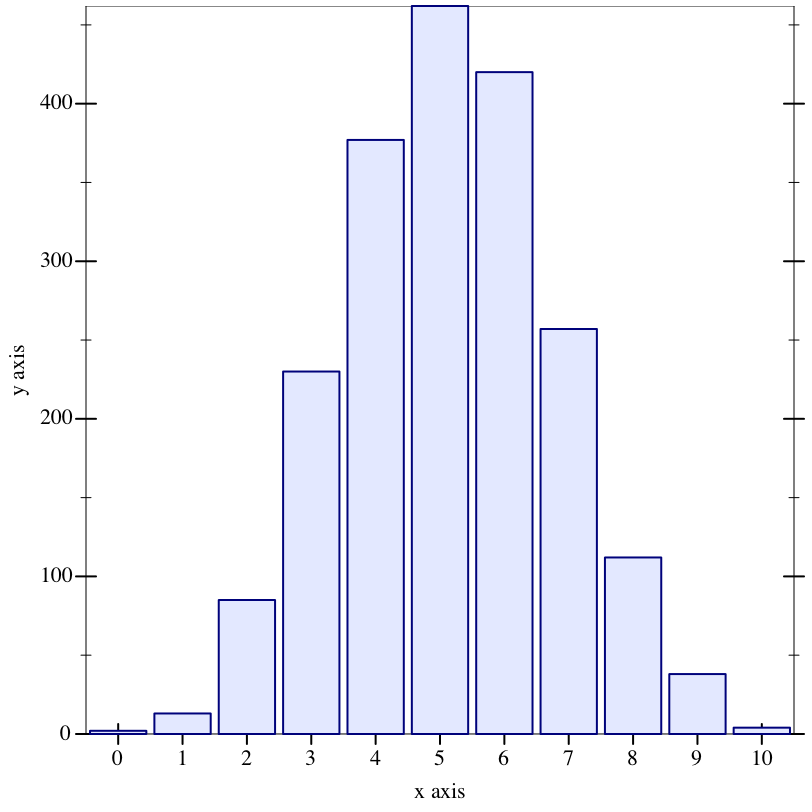
Examples: | |||||||||||||||||||||||||
|
syntax
(importance-sampler def/expr ... result-expr)
5.3 Metropolis-Hastings Sampler and Transitions
Metropolis-Hastings (MH) is an algorithm framework for producing a correlated sequence of samples where each sample is based on the previous. The algorithm is parameterized by the mechanism for proposing a new state given the previous state; given a proposal, the MH algorithm accepts or rejects it based on how the proposal was generated and the relative likelihood of the proposed state.
The mh-sampler form implements the Metropolis-Hastings framework, and the proposal mechanisms are implemented by a variety of MH transition types.
syntax
(mh-sampler maybe-transition def/expr ... result-expr)
maybe-transition =
| #:transition transition-expr
The transition-expr determines the mechanism used to propose new states. If absent, (single-site) is used.
Examples: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5.3.1 Metropolis-Hastings Transitions
procedure
(mh-transition? v) → boolean?
v : any/c
procedure
(single-site [proposal #:zone zone-pattern]) → mh-transition?
proposal : (or/c proposal? (-> proposal?)) = (default-proposal) zone-pattern : any/c = #f
A zone pattern matches a zone if the two values are equal? or if the zone pattern is #f.
procedure
(multi-site [proposal #:zone zone-pattern]) → mh-transition?
proposal : (or/c proposal? (-> proposal?)) = (default-proposal) zone-pattern : any/c = #f
procedure
(slice [ #:scale scale-factor #:zone zone-pattern]) → mh-transition? scale-factor : (>/c 0) = 1 zone-pattern : any/c = #f
The scale-factor argument controls the width parameter used to find the slice bounds.
procedure
(enumerative-gibbs [#:zone zone-pattern]) → mh-transition?
zone-pattern : any/c = #f
Note: unlike traditional Gibbs sampling, this transition picks a choice at random rather than perturbing all choices round-robin.
procedure
(cycle tx ...+) → mh-transition?
tx : mh-transition?
procedure
(mixture txs [weights]) → mh-transition?
txs : (listof mh-transition?) weights : (listof (>/c 0)) = (map (lambda (tx) 1) txs)
procedure
(rerun) → mh-transition?
5.3.2 Metropolis-Hastings Proposals
The single-site and multi-site transitions are parameterized by the proposal distribution used to perturb a single random choice.
procedure
procedure
parameter
(default-proposal) → (or/c proposal? (-> proposal?))
(default-proposal proposal) → void? proposal : (or/c proposal? (-> proposal?))
The initial value is proposal:drift.
5.3.3 Zones: Identifying Random Choices
Random choices made during the execution of a model can be grouped into zones using the with-zone form. Specialized transitions can then be assigned to choices based on their membership in zones.
syntax
(with-zone zone-expr body ...+)
5.4 Particle Filters
A particle set consists of a collection of particles, each of which contains a current state estimate and a likelihood weight. Particle sets are updated via a (stochastic) state transformer that produces a new state for each particle. Observations performed by the state transformer adjust the particles’ weights.
procedure
(particles? v) → boolean?
v : any/c
procedure
(make-particles n init-state) → particles?
n : exact-nonnegative-integer? init-state : any/c
procedure
ps : particles?
procedure
(particles-update ps update-state) → particles?
ps : particles? update-state : (-> any/c any/c)
procedure
(particles-score ps score-state) → particles?
ps : particles? score-state : (-> any/c any)
Equivalent to (particles-update ps (lambda (st) (score-state st) st)).
procedure
(particles-resample ps [n #:alg algorithm]) → particles?
ps : particles? n : exact-nonnegative-integer? = (particles-count ps) algorithm : (or/c 'multinomial 'residual #f) = 'multinomial
procedure
(particles-effective-count ps) → real?
ps : particles?
procedure
(particles-effective-ratio ps) → real?
ps : particles?
procedure
→ (vectorof (cons/c any/c (>/c 0))) ps : particles?
procedure
(particles-states ps) → vector?
ps : particles?
In general, it is only sensible to call this function when the weights are known to be equal, such as after calling particles-resample.
procedure
(in-particles ps) → sequence?
ps : particles?
5.5 Enumeration Solver
syntax
(enumerate maybe-limit maybe-normalize def/expr ... result-expr)
maybe-limit =
| #:limit limit-expr maybe-normalize =
| #:normalize? normalize?-expr
limit-expr : (or/c #f (>=/c 0))
normalize?-expr : any/c
The enumerate form works by exploring all possibilities using
the technique described in [EPP]. If limit-expr is
absent or evaluates to #f, then exploration ceases only when
all paths have been explored; if any path is infinite, then
enumerate fails to terminate. If limit-expr is
given and evaluates to a probability limit, then exploration
ceases when the error of the normalized result distribution would be
less than limit—
Only discrete and integer-valued distributions can be sampled with enumerate, and infinite-range distributions (such as geometric-dist) and infinitely-deep recursive functions (such as geometric) require the use of #:limit for termination.
Example: | |||||||
|
Use #:limit to control when exploration should be cut off.
> (enumerate #:limit 1e-06 (geom))
(discrete-dist
[0 524288/1048575]
[1 262144/1048575]
[2 131072/1048575]
[3 65536/1048575]
[4 32768/1048575]
[5 16384/1048575]
[6 8192/1048575]
[7 4096/1048575]
[8 2048/1048575]
[9 1024/1048575]
[10 512/1048575]
[11 256/1048575]
[12 128/1048575]
[13 64/1048575]
[14 32/1048575]
[15 16/1048575]
[16 8/1048575]
[17 4/1048575]
[18 2/1048575]
[19 1/1048575])
Use #:normalize? #f to get the result probabilities without normalizing by the acceptance rate:
> (enumerate #:normalize? #f (define (drop-coin?) (flip 0.9)) (define (drunk-flips n) (cond [(zero? n) #t] [(drop-coin?) 'failed] [else (and (flip) (drunk-flips (sub1 n)))])) (define A (drunk-flips 10)) (observe/fail (not (eq? A 'failed))) (eq? A #t)) (discrete-measure [#f 1.0] [#t 1.855468750000192e-12])